IntervalLinearAlgebra.jl: Linear algebra done rigorously
Hello! Google Summer of Code is almost over and in this blog post I will summarize the final results of the project. First of all some useful facts.
Project goals: By the proposal, the goal of the project was to develop
IntervalLinearAlgebra.jla package for numerical linear algebra using interval arithmetic. Particularly, the goal for the package was to be able to solve interval linear systems and compute fast interval multiplication using Rump algorithm.Deliverable: The main deliverable is the project repository, available here
JuliaCon 2021: I also presented my work at JuliaCon2021 the annual conference about Julia. Here is the video for you to enjoy. (Youtube didn't like my accent and refused to generate captions for the video, nevertheless I transcribed the whole video for you 😃 )
Documentation: The package has also its own documentation page. At the moment it has a full API interface documentationn, a beginner tutorial and some articles explaining the theory of interval linear algebra. I am particularly proud of this article and the layout I designed for the references page. The post-GSoC goal for the documentation is to become the most complete yet accessible reference about interval linear algebra.
Some statistics
According to good coding practices, most of the work has been done through pull requests, in total 51 closed PRs and 2 open. Huge thanks to my mentors Marcelo Forets and David Sanders for the patience in reviewing those.
7 people starred the package. Funnily enough, the repository with the juliacon talk slides has more stars at the time of writing.
According to codecov, at the time of writing the package has 310 effective lines of code (removing all comments and all dummy lines such as
end,function func_name, empty lines etc.)The two currently open PRs about eigenvalues are adding 77 effective lines of code
According to codecov, package coverage is 97%.
Since the package uses IntervalArithmetic.jl as back-end for interval computations, it was only fair for me to also contribute in IntervalArithmetic.jl development. Hence, during the bonding period I tried to give my two cents to help the package achieve the IEEE-1788 standard compliance. Here is a summary of my contributions to IntervalArithmetic.jl
I created the repository ITF1788.jl. ITF1788 is a test suite (available here) which can be used to verify an implementation of interval arithmetic is compliant with the standards. The tests are written in their own domain specific language called ITL. ITF1788.jl parses the tests written in ITL and generates julia code from them.
This tool will hopefully help achieve standard compliance one day.
Using the above developed tool, I could generate all tests in Julia and opened this meta issue tracking what is missing to be compliant with the standard.
one PR fixing some issues with bare interval constructors (merged)
one PR fixing issues with decorated interval constructors (still WIP)
one PR fixing issues with reverse operations
one PR adding some missing operations for complex intervals
Hopefully, I will keep helping in contribution to IntervalArithmetic.jl, but now let us talk about the main beef: IntervalLinearAlgebra.jl
Tour of package features
Linear Systems
IntervalLinearAlgebra.jl offers an user-friendly interface to solve interval linear systems with different algorithms and techniques. An interval system is a linear system \(\mathbf{Ax}=\mathbf{b}\) where \(\mathbf{A}\) and \(\mathbf{b}\) are interval matrix and vector, respectively. The main function to solve interval linear system is solve, which allows to choose the algorithm and the preconditioning mechanism. Here is a quick example
using IntervalLinearAlgebra, LazySets, Plots
A = [2..4 -1..1;-1..1 2..4]
b = [-2..2, -1..1]
Xenclose = solve(A, b, GaussianElimination())
polytopes = solve(A, b, LinearOettliPrager())
plot(UnionSetArray(polytopes), ratio=1, label="solution set", legend=:top)
plot!(IntervalBox(Xenclose), label="enclosure")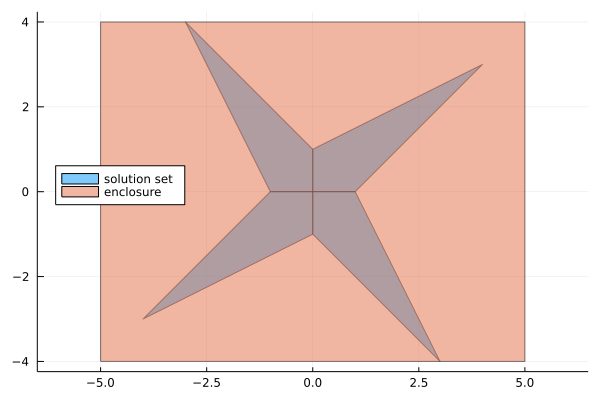
The LinearOettliPrager solver uses Oettli-Präger theorem to find an exact characterization of the solution set (which is composed by an union of convex polytopes, which are internally represented using LazySets.jl). This is ok for lower dimensions, but as finding the solution set has exponential complexity, it becomes unfeasible in higher dimensions. For this reason there are polynomial time algorithms (such as GaussianElimination) to compute an interval enclosure of the solution set. It is good to notice, however, that this enclosure may be strictly larger than the hull of the solution set, whose computation also has exponential complexity.
Matrix multiplication
The second goal of the project was to implement the Rump fast multiplication algorithm (see this paper for more details). The main idea of Rump algorithm to to reduce interval matrix multiplication to floating point matrix multiplication, allowing to exploit optimised BLAS routines. In the package, you can use the function set_multiplication_mode to set the algorithm you want to use. For example
set_multiplication_mode(:fast)will set to use Rump fast multiplication algorithm (default behavior). While
set_multiplication_mode(:slow)will set to use the traditional matrix multiplication algorithm. With an interface to easily switch between multiplication modes, we can perform some benchmarks.
The following picture gives an intuitive idea of the speed-up obtained. A more detailed analysis coming soon to the documentation!
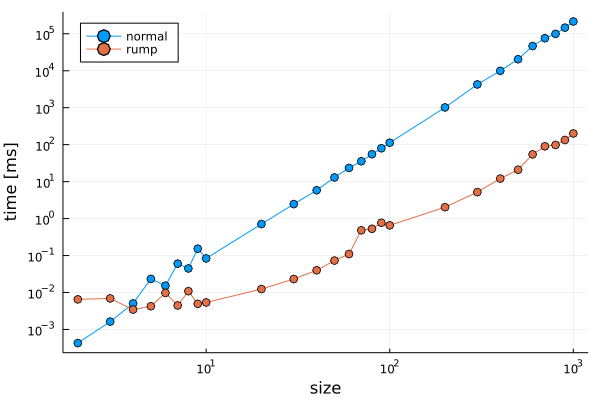
Rump multiplication algorithm is significantly faster than the traditional multiplication algorithm. As a price to pay, if both matrices are interval matrices (that is both matrices have intervals with non-zero radius), then Rump algorithm may produce larger intervals than the traditional multiplication algorithm. This overestimate, which can be 50% at maximum, is at the worst when the radii and centers of the intervals in the matrix have the same oder of magnitude. In the next picture, on the x-axis we have the mean ratio between radius and midpoint in absolute value. The y-axis measure the percentual overwidth of intervals obtained with Rump fast multiplication with respect to the traditional multiplication algorithm.
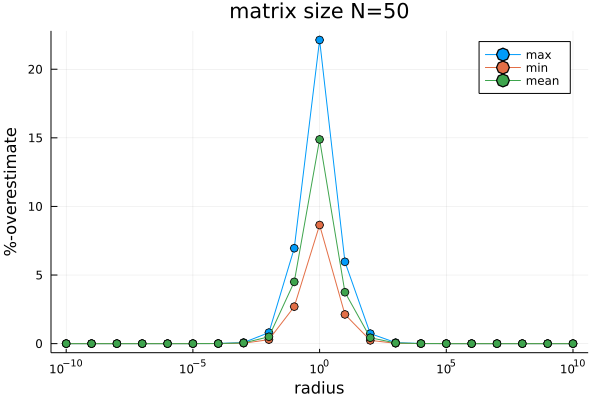
Eigenvalues
This was a stretch goal in the original proposal, but I'm glad I got something done. At the moment, I have two PRs open regarding eigenvalues.
The first one computes rigorously the eigenvalues and eigenvectors of a real matrix. That is, given a floating point matrix \(A\), it starts by approximated eigenvalues and eigenvectors \(\tilde{\lambda}\) and \(\tilde{\vec{x}}\) and returns intervals guaranteed to contain the true eigenvalue \(\lambda\) and an interval vector guaranteed to contain the true eigenvector \(\mathbf{x}\). Here is a short example
julia> A = Symmetric([1 2;2 3])
2×2 Symmetric{Int64, Matrix{Int64}}:
1 2
2 3
julia> evals, evecs, cert = verify_eigen(A);
julia> evals
2-element Vector{Interval{Float64}}:
[-0.236068, -0.236067]
[4.23606, 4.23607]
julia> evecs
2×2 Matrix{Interval{Float64}}:
[-0.850651, -0.85065] [0.525731, 0.525732]
[0.525731, 0.525732] [0.85065, 0.850651]
julia> cert
2-element Vector{Bool}:
1
1The interval arrays evals and evecs contain bounds for the eigenvalues and eigenvectors of \(A\), respectively. The vector cert is a boolean array of certificates, if cert[i] == true, then the bounds for the ith eigenvalue and eigenvector of \(A\) are guaranteed to contain the true eigenvalue and eigenvector.
The second one is about bounding all eigenvalues of an interval matrix. Here is a quick example
A = [-3.. -2 4..5 4..6 -1..1.5;
-4.. -3 -4.. -3 -4.. -3 1..2;
-5.. -4 2..3 -5.. -4 -1..0;
-1..0.1 0..1 1..2 -4..2.5]
eigenbox(A)[-8.8221, 3.4408] + [-10.7497, 10.7497]imThe function eigenbox takes a interval matrix and finds a complex interval that contains all \(\lambda\in\mathbb{C}\) that are eigenvalues of some \(A\in\mathbf{A}\). The following picture shows the eigenvalues of the previous matrix in the complex plane, obtained by Monte Carlo simulation, and the computed enclosure.
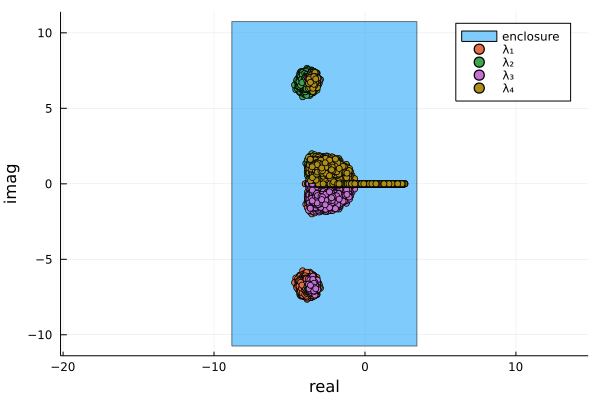
Future goals
Once the above mentioned PRs about eigenvalues are merged, the first version of the package will be released! 🎉 This should happen within one week, stay tuned!
The main feature I want to add to the package is a solver for parametric interval linear systems. A parametric interval linear system has the form \(\mathbf{A(p)x}=\mathbf{b(p)}\), where \(\mathbf{p}\) is a set of parameters. For example
\[ \begin{bmatrix} p_1&p_2\\ p_2+1&p_1 \end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}\frac{p_1+6p_2}{5}\\2p_1-6\end{bmatrix} \]where \(p_1\in[2, 4]\) and \(p_2\in[-2, 1]\). What makes this kind of problem exciting is that just substituting the intervals in the equations and solving the normal interval linear system would lead to great overestimation, due to the so called dependency problem that interval arithmetic suffers from. For this reason, some special algorithms are needed to treat these kind of problems. Parametric interval linear arise very often in engineering applications. For example, a system with the structure above could occur when solving a resistive circuit using nodal analysis or in Finite Element Method (FEM).
Other enhancement for the package could be
extend the linear systems solver interface to work also with complex intervals
add algorithms for overdetermined linear systems
add specialized algorithms to verify eigenvalues and eigenvectors of floating point matrices with special structure (symmetric, persymmetric, Toeplitz)
bound eigenvectors of interval matrices
spectral decomposition of interval matrices
interval version of matrix functions (square root, logarithm, exponential etc.)
the ultimate goal of the package being Linear algebra done rigorously.
Final thoughts
Over all, Google Summer of Code has been a lot of fun, I have learned a lot and greatly developed my coding and project management skills. The best thing was to learn some "advanced"(?) tips and tricks from my mentors that otherwise I couldn't have learned by just reading the julia documentation. I am very grateful to my mentors Marcelo Forets and David Sanders for their patience and support. Moreover, special thanks to the Julia community for offering a very welcoming environment. I am looking forward to collaborating in great projects with great people!.
